Table of Contents
Generating Sine Tables from Parabolas
by White Flame
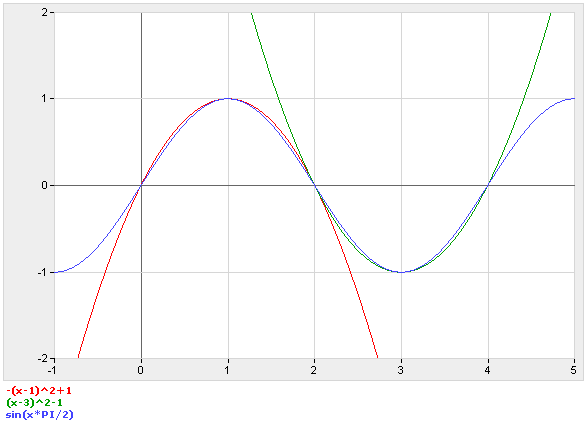
It's been a long-standing tradition in games & demos that sine waves can be approximated by parabolas (see the graph at the bottom). They're a little boxier, and deviate to an error of about 6%, but generally work for doing quick and dirty trig.
Parabolas are easy to generate, as they can represent a value under constant acceleration, which is discretely defined as
loop { x += dx dx += Constant }
Here's a simple implementation ripped from from Too(C)o(M)p(L)ex by Cruzer/Camelot, and adjusted a bit for clarity. The original source is in the download from the CSDb page, and uses self-modifying code to hold the value and delta.
; ca65 syntax initSineTable: ldy #$3f ldx #$00 ; Accumulate the delta (normal 16-bit addition) : lda value clc adc delta sta value lda value+1 adc delta+1 sta value+1 ; Reflect the value around for a sine wave sta sine+$c0,x sta sine+$80,y eor #$ff sta sine+$40,x sta sine+$00,y ; Increase the delta, which creates the "acceleration" for a parabola lda delta adc #$10 ; this value adds up to the proper amplitude sta delta bcc :+ inc delta+1 : ; Loop inx dey bpl :-- rts value: .word 0 delta: .word 0 sine: .res 256
Notes on the code
Precision
The accelerating value we calculate is held in a 16-bit number, the high byte of which we will use to fill in the values in the 0-255 sine table. This is required, as when the curve is on its more “flat” regions, the delta is much less than 1/256th of the amplitude (what a single byte can hold).
A piece at a time
The outer loop only spans 1/4th of the period (ie, 0-1 from the graph), as each quarter can be reflected onto the other. As the value accelerates from 0-127, it's stored mirrored around $c0 (x=3 on the graph), while the inverted value is mirrored around $40 (x=1 on the graph). It uses an incrementing .X and decrementing .Y to accomplish the mirroring.
Output values
The final table follows the same shape as the graph, going through this progression:
- table + $00 = ~$80
- table + $40 = $ff
- table + $80 = ~$80
- table + $c0 = $00
- table + $ff = ~$80
Thus, the sine values are unsigned with a DC offset of $80.
Modifications
Cosine instead of Sine
Simply change how the output is written:
; Reflect the value around for a cosine wave sta sine+$80,x sta sine+$40,y eor #$ff sta sine+$00,x sta sine+$c0,y
Amplitude
If you want a range of $00-$7f instead of $00-$ff (as is in the original demo):
- change the EOR value from #$ff to #$7f
- change the delta acceleration from #$10 to #$08
Any base-2 amplitude should be likewise possible.